DWITIYA SOPAN
Compass
MARLINE SPIKE HITCH
MARLINE SPIKE HITCH
MARLINE SPIKE HITCH 01
MARLINE SPIKE HITCH 02
SQUARE LASHING
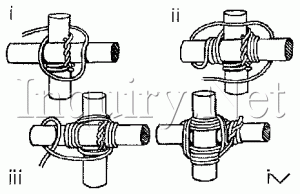
SQUARE LASHING
SQUARE LASHING
Square lashings are used to bind together two spars that are at right angles with one another.
i) Place the poles on the ground in the shape of a cross. Tie a clove hitch around the bottom pole near the crosspiece. Twist the free end of the rope around its standing part and tuck it out of the way.
ii) Make three or four wraps around the spars, keeping the rope very tight. As you form the wraps, lay the rope on the outside of each previous turn around the crosspiece, and on the inside of each previous turn around the bottom pole.
iii) Then wind three or four frapping turns around the wrapping to tighten the lashing as much as you can.
iv) Finish it off with another clove hitch.
ii) Make three or four wraps around the spars, keeping the rope very tight. As you form the wraps, lay the rope on the outside of each previous turn around the crosspiece, and on the inside of each previous turn around the bottom pole.
iii) Then wind three or four frapping turns around the wrapping to tighten the lashing as much as you can.
iv) Finish it off with another clove hitch.
ESTIMATION – HEIGHT AND DISTANCE
ESTIMATION – HEIGHT AND DISTANCE
ESTIMATION – DISTANCE AND HEIGHT
ESTIMATION – DISTANCE AND HEIGHT
ESTIMATION - 01
ESTIMATION - 02
ESTIMATION - 03
ESTIMATION
ESTIMATION
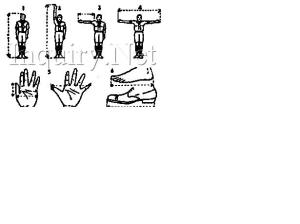
Learning to Judge Distance
As a means of checking your estimates, learn the exact length of your pace. If fairly tall, learn to pace an exact yard, heel to heel. On a quiet road, in a field, or out on the prairie, begin judging short distances to various objects, then pacing to check your “guess.” Gradually increase the distances. Do this in competition with several other Scouts and you’ll find it an interesting game. Remember that the eye measures distance as in an “air line,” from eye to object, and does not allow for irregularities of the ground. In other words, ground distance may be greater than visual distance.
PERSONAL MEASUREMENT
As an aid in making short measurements you should know a number of your personal measurements. Your known hand-span will often be particularly useful. If fully developed your measurements will be close to this:
| Breadth of thumb, and nail joint of forefinger = 1 inch (2.54 centimeters). | |
| Span of the thumb and forefinger = 6.5″ (or 17 centimeters). | |
| Span of thumb and any other finger = 8.5″ (or 21.6 centimeters). | |
| Wrist to elbow = 10″ (or 25 centimeters). | |
| Elbow to tip of forefinger = 17″ (or 43 centimeters). | |
| Your reach, arms out-stretched, will nearly equal your height. |
Some Further Hints
| At 1/2 mile or approximately 880 yards (or 800 meters) a man looks a post. | |
| At 770 yards (or 700 meters) the head is not yet visible. | |
| At 660 yards (or 600 meters) the head is visible as a dot. | |
| At 550 yards (or 500 meters) the shoulders appear bottle shaped. | |
| At 1/4 mile, or approximately 440 yards (or 400 meters) movements of the legs can be seen. | |
| At 330 yards (or 300 meters) the face can be seen. | |
| At 220 yards (or 200 meters) buttons and details of clothing are recognizable. | |
| At 110 yards (or 100 meters) eyes and mouth can be seen clearly. |
To estimate greater distances, judge the farthest probable distance, then the nearest possible, and “split the difference.”
IMPROVISED STRETCHER
MAKING IMPROVISED STRETCHER
USING BLANKLETS AND POLES
IMPRPOVISED STRETCHER USING BLANKLETS AND POLES
USING ROPES
IMPROVISED STRETCHER USING ROPE
A PPT ON MAKING IMPROVISED STRETCHERS
FINDING NORTH BY CONSTELLATIONS
FINDING NORTH BY CONSTELLATIONS
Star Method.
(1) Less than 60 of approximately 5,000 stars visible to the eye are used by navigators. The stars seen as we look up at the sky at night are not evenly scattered across the whole sky. Instead they are in groups called constellations.
(2) The constellations that we see depends partly on where we are located on the earth, the time of the year, and the time of the night. The night changes with the seasons because of the journey of the earth around the sun, and it also changes from hour to hour because the turning of the earth makes some constellations seem to travel in a circle. But there is one star that is in almost exactly the same place in the sky all night long every night. It is the North Star, also known as the Polar Star or Polaris.
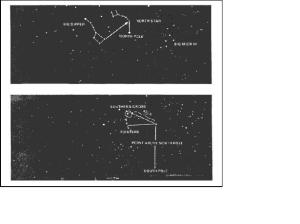
(3) The North Star is less than 1° off true north and does not move from its place because the axis of the earth is pointed toward it. The North Star is in the group of stars called the Little Dipper. It is the last star in the handle of the dipper. There are two stars in the Big Dipper, which are a big help when trying to find the North Star. They are called the Pointers, and an imaginary line drawn through them five times their distance points to the North Star. There are many stars brighter than the North Star, but none is more important because of its location. However, the North Star can only be seen in the northern hemisphere so it cannot serve as a guide south of the equator. The farther one goes north, the higher the North Star is in the sky, and above latitude 70°, it is too high in the sky to be useful (Figure 9-9).
FIGURE 9.9
Figure 9-9. Determining direction by the North Star and Southern Cross.
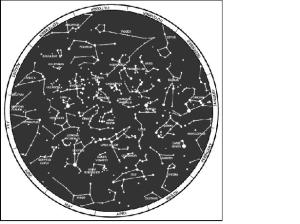
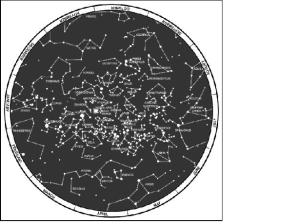
(4) Depending on the star selected for navigation, azimuth checks are necessary. A star near the north horizon serves for about half an hour. When moving south, azimuth checks should be made every 15 minutes. When traveling east or west, the difficulty of staying on azimuth is caused more by the likelihood of the star climbing too high in the sky or losing itself behind the western horizon than it is by the star changing direction angle. When this happens, it is necessary to change to another guide star. The Southern Cross is the main constellation used as a guide south of the equator, and the above general directions for using north and south stars are reversed. When navigating using the stars as guides, the user must know the different constellation shapes and their locations throughout the world (Figure 9-10 and Figure 9-11).
Figure 9-10. Constellations, northern hemisphere.
FIGURE 9.10
Figure 9-11. Constellations, southern hemisphere.
FIGURE 9.11
SCOUT PACE
Pace (unit)
A pace (or double-pace or passus) is a measure of distance used in Ancient Rome. It is the measure of a full stride from the position of the heel when it is raised from the ground to the point the same heel is set down again at the end of the step. Thus, a distance can be “paced off” by counting each time the same heel touches ground, or, in other words, every other step. In Rome, this unit was standardized as two gradūs or five Roman feet (about 1.48 metres or 58.1 Englishinches). There are 1000 passus in one mille, and a mille was sometimes referred to as a mille passus.
A pace in modern terminology is usually taken as being a single pace rather than a double pace. It has no formal definition but is taken as being around 30 inches
COMPASS BEARING
Bearings |
| A directional compass is shown below. It is used to find a direction or bearing.
The four main directions of a compass are known as cardinal points. They are north (N), east (E), south (S) and west (W). Sometimes, the half-cardinal points of north-east (NE), north-west (NW), south-east (SE) and south-west (SW) are shown on the compass. The above compass shows degree measurements from 0° to 360° in 10° intervals with:
When using a directional compass, hold the compass so that the point marked north points directly away from you. Note that the magnetic needle always points to the north.
Bearing
The true bearing to a point is the angle measured in degrees in a clockwise direction from the north line. We will refer to the true bearing simply as the bearing.
For example, the bearing of point P is 065º which is the number of degrees in the angle measured in a clockwise direction from the north line to the line joining the centre of the compass at O with the point P (i.e. OP).
The bearing of point Q is 300º which is the number of degrees in the angle measured in a clockwise direction from the north line to the line joining the centre of the compass at O with the point Q (i.e. OQ).
Note:
The bearing of a point is the number of degrees in the angle measured in a clockwise direction from the north line to the line joining the centre of the compass with the point.
A bearing is used to represent the direction of one point relative to another point.
For example, the bearing of A from B is 065º. The bearing of B from A is 245º.
Note:
|
No comments:
Post a Comment